Aquí tienes más información sobre Octave: Wikipedia.
Nosotros utilizaremos la versión que ha desarrollado la escuela de caminos de la Universidad Politéctica de Madrid (UPM). Este es el link para la descarga:
Si el enlace anterior no funciona puedes probar con el siguiente:
Versión online
Si no deseamos instalar Octave en nuestro ordenador disponemos de una versión online disponible en la siguiente dirección.Escribir una matriz
Veamos cómo podemos escribir y operar con matrices en Octave.Para escribir la matriz A de orden 3x3 podemos escribir por filas, separando cada fila por punto y coma y separando cada elemento por un espacio.
A=[1 -2 0;2 -5 -1;3 0 -3]
Octave responde mostrándonos la matriz A perfectamente ordenada por filas y columnas.
También se podrían separar los elementos de cada fila por comas y no por espacios.
Determinante de una matriz
Podemos calcular el determinante de la matriz A que es 9.det(A)
Matriz de números aleatorios
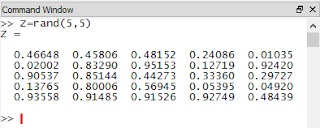
Podemos crear la matriz Z de orden 4x4 creada por números aleatorios.Z=rand(5,5)
Limpiar pantalla
clcCalcular la inversa de una matriz
Calculemos la matriz inversa de A.A^-1
Resolución de un sistema compatible determinado
Tomemos la matriz A anterior que tiene determinante distinto de cero y junto con el vector columna B siguiente montemos un sistema de ecuaciones con solución única.El vector columna B es el siguiente.
B=[-3;-7;6]
Creamos el sistema matricial siguiente.
AX=B
Despejamos X.
X=A-1B
Si el vector X tiene por componentes \(x_1, x_2, x_3\) podemos afirmar que la solución del sistema es:
\[x_1=1\] \[x_2=2\] \[x_3=-1\]







No hay comentarios:
Publicar un comentario